CAESES 全参数化建模及优化软件

CAESES 提供了多种 DoE 及优化算法，其中 DoE 的方法包括 Design Lab、Design Assembler、Ensemble Investigation、Exhaustive Search、 Sobol。

在 DoE 中，给定需要考虑的变量，通过不同的方法组合这些变量不同的值， 得到新的模型，然后通过计算得到目标函数值，之后便可以分析这些变量 对目标函数值得影响，便可以进一步确定进一步的优化中哪些变量是必要 的，哪些变量是不必要的，以及变量的范围。

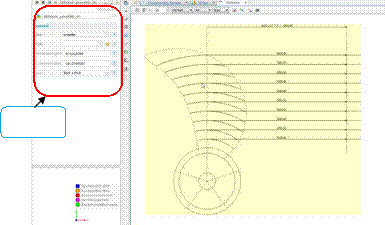
DesignLab：在这种方法中，给定需考虑的变量以及范围，便可以通过调整 进度条的形式来改变变量数值，同时可以通过 3D 视图实时观察模型几何变 化，如下图所示。然后通过手动点击生成的方式确定需要计算的模型。

DesignAssembler：这种方法中可以直接手动给定每个变量的数值，或者直 接导入.CSV 文件来给定，如下图所示。

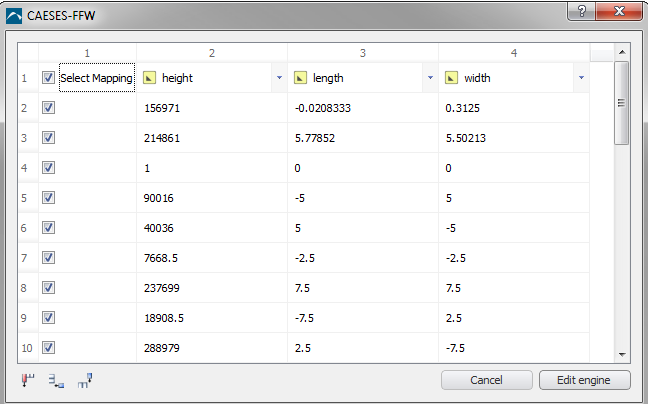
EnsembleInvestigation：这种方法中，可以通过一定的格式给定变量一系列的值，如：可以给定离散的不同数值[1,3,6,10,15,21]，就会生成变量值为 1、3、6、10、

15、21 时的模型；或者给定[0,2..20],这样就会生成变量值为 0、2、4、6 一直到 20 时的模型。

ExhaustiveSearch  ：这种方法中给定每个变量的范围以及等分的点数，之后将等分后的变量值的所有组合列举出来。如变量 A 范围为[1,3],变量 B 范围为[1,5],等分为 3 份，即变量 A 的值为 1、2、3，变量 B 的值为 1、3、5，则所有新模型组合为[1,1]、[1,3]、[1,5]、[2,1]、[2,3]、[2,5]、[3,1]、[3,3]、[3,5]。

Sobol：这种方法中给定变量的范围，并给定需要生成模型的总数，之后通过一种随机的算法生成组合。Sobol 是一种常用的具有较好收敛性的随机序列算法，是在 CAESES 中较为常用的一种 DoE 方法。

优化算法有：Brent、NelderMeadSimplex、TSearch、NewtonRaphson、

Nsga2、Mosa

Brent ：这种算法使用 Brent 一维最小化算法来寻找一个自由变量范围内的最小函数值。Brent  方法在函数合适时会使用抛物线差值迭代的方法，而函数不合适的时候使用黄金分割搜索方法。这种方法通过迭代寻找给定的精度允许范围内的函数最小值。但这种方法并不用在通常的优化任务，比如有 CFD 参与的优化任务。因为它只能用于单变量的优化，类似于 Newton Raphson 方法，Brent 方法通常用于几何优化任务，例如寻找到一点最短的距离等。

Nelder Mead Simplex：这种方法是由 Nelder 和 Mead 提出的算法，可称为下山单纯形法，类似于一种搜索方法，这种方法只是对函数求值，这是一种可以包含不等式约束的单目标算法。

单纯形是一种几何图形组合，对于 N 维而言，就是由 N+1 个点（或顶点），点之间的连线以及多边形面组成。二维中，单纯形是三角形，三维空间中就是四面体等等。据推测，单纯形是非退化的，这意味着单纯形所有的边在 N 维空间中都不与其他边平行，例如三角形没有平行边。单纯形在设计空间内移动来寻找最小值（至少是当地的），移动形式包括反射、放大及缩小。对于 N 维空间最小化，下山单纯形法必须通过 N+1 个点来定义初始单纯形。通常，初始的潜在的 N+1 个候选设计从之前的 DoE 序列（例如 Sobol 方法得到的序列）。之后下山单纯形法就会通过自己的方法遍历设计空间。下山单纯形法在它需要求值的函数数量方面不是很有优势。但当仅需要针对某个问题快速获得解决方案且需要计算负担较小时，这种方法通常来说也不失为一种上佳的方法。下山单纯形法通常被认为一种强大的单目标优

化方法。

TSearch：

Tangent  Search 方法对于包含不等约束的小规模、单目标优化方法。这种方法的主要特点是检测解空间内下降的搜索方向，来确保能够快速的修正搜索方向并且保证在可行区域内搜索。

首先在允许的解空间内运用直接搜索方法，并且包括在变量轴上进行的从所谓的基点开始的探索性搜索；之后在成功的探索性搜索中寻找到的下降搜索方向基础上进行全局搜索。这种方法能够寻找到 N*V 空间（维数取决于自由变量的数量）解空间内的一个当地最小值。一个下降搜索的方向由最多求 2*N*V 个函数的值来决定。自由变量需要给定确定的上限及下限。要想得到满意的结果，一般需要设定初始步长为相应变量范围的 5%-10%。最小步长大约为初始步长的 5%-10%。Tangent  Search 方法对于很多优化任务都是一种可靠地方法，经常与 Sobol方法联合使用，用 Sobol 方法得到的 DoE 结果作为初始设计。

NewtonRaphson：牛顿-拉夫逊方法也即牛顿迭代法属于梯度法的范畴。这种方法依赖于对于目标函数的局部二阶近似。这是一种单目标算法，通过二次偏导例如目标函数的 Hessian  矩阵来实现对目标函数的近似。这种算法是一种迭代算法。通常，这种算法不用于复杂的优化任务，类似 Brent 算法，对于几何和代数优化任务十分有效，例如距离平方的最小化。

Nsga2：

NSGA-Ⅱ (Non-dominated Sorting Genetic Algorithm II)  即为第二代非支配排序遗传算法，是目前最流行的多目标进化算法之一，实现了著名的基于非支配排序的多目标进化算法。它需要设定世代数、人口数量、变异概率及交叉概率。交叉概率影响父母产生孩子时的基因混合过程，如果这个值为 0，一个单亲的基因就会复制到孩子身上，而与另一个母本的基因没有交叉。这种算法对于一些互相冲突的目标需要最小化（不止一个目标最小）的任务十分有效，而且也可以考虑不等式约束。

Mosa：

MOSA 方法全称 Dominance-Based Multi-Objective Simulated Annealing（显性 多目标模拟退火算法），是普通的单目标模拟退火方法（SA）的一个扩展版 本。SA 方法的理念是热力学原理的类比，慢慢冷却的金属会采用低能量的 结晶状态，而与此不同的是，如果液态金属迅速冷就不会达到最小状态， 它们遵循玻尔兹曼概率分布。 这种方法在每一个历元生成一定数量的样本（也称为持续时间），并且使用 固定的系统温度。当一个历元结束后，温度变低，然后生成新的样本，并 反复进行。样本设定为只受一个设计变量的影响，并且这个变量是随机选 择的，而且通过拉普拉斯分布的平均值影响样本。在这里，西格玛特性决 定影响的缩放因子及幅度大小。MOSA 方法适用于多目标优化，并且能够 考虑不等式约束。

除了从设计引擎自动生成结果表之外，用户可以自由地调用任何设计数据来组装自己的表格。

步骤：

1. 选择菜单栏> view >new > viewer > design results table.

从对象树中选择设计、参数、设计变量和约束，并通过拖放将其移动到创建的表格中。这个过程也可以单独对不同的对象进行处理。此外，从对象树中的设计分支中选择设计，并将它们拖到表格中，以便将它们添加进去。

为了方便创建工程图，需要使用2D窗口的创建功能。

步骤：

1. 选择菜单栏> view > new > 2D window setup

2.简单地拖拽螺旋桨模型进入2D场景

、

3.对于配置， 在2D窗口中选择项目，以便可以在对象编辑器中更改属性。您可以在对象编辑器（“视图”属性）中为所选螺旋桨选择要绘制的内容（即在2D窗口中选择）。

 
4.缩放、纸张尺寸修改和其他功能也可以应用于螺旋桨。

Cartesian Shift transformation

笛卡尔变形为给定曲面创建波浪状变形，类似余弦的变形函数在球形空间中被定义，然后独立地应用于x，y和z坐标。该函数在径向方向上关于源项 位置逐渐消退。

步骤：

1. 选择工具条> transformations > shifts > cartesian shift.

2. 设置source向量, 例如一个点特征；

3. 可以认为源向点在余弦函数的中心或者在修改区域的边界处相位延迟，设置centralized集点控制改变效果；

4. 设置变形的幅度值Amplitude；

5. 设置XYZ坐标是否受变形影响，例如上图，只有曲面上的Z坐标得到了变形；

请参考名称为“myScript.fsc”的示例脚本中的内容，该脚本的内容是打开项目文件，更改设计变量的某些值，并将生成的新几何模型导出为STL数据：

//打开模型文件

openProject("C:\fw\myProject.fdb")

// 改变一些对象内容，此处修改设计变量

|designvariables| width.setValue(0.50)

|designvariables|radius.setValue(0.25)

// 输出新的STL 模型曲面

FexportColourStl.export("geom.stl")

//退出软件

exit(true) 

请注意，项目中的每个对象（而不仅仅是设计变量）都可以使用特定命令进行寻址和更改

批量调用

最后，使用以下命令在批处理模式下运行CAESES：

Windows系统：

Framework_crt.exe myScript.fsc

Linux系统：

Framework_crt.sh myScript.fsc